The Elegant Way To Generate The Complex Number Field

The Elegant Way To Generate The Complex Number Field

Definition: A ring <R, +, •> is a set R together with two binary operations + and • of addition and multiplication defined on R such that the following axioms are satisfied:
1) <R, +> is an abelian group.
2) Multiplication is closed and associative.
3) For all a, b, c contained in R, the left distributive law, a(b + c) = (ab) + (ac), and the right distributive law, (a + b) = (ac) + (bc), hold.

Definition: A ring in which the multiplication is commutative is a commutative ring. A ring R with a multiplicative identity 1 such that 1x = x1 = x for all x contained in R is a ring with unity. A multiplicative identity in a ring is unity, and this unity is unique.

Definition: If a and b are two nonzero elements of a ring R such that a•b = 0, then a and b are divisors of zero.

Definition: An integral domain is a commutative ring with unity containing no divisors of zero.

If an integral domain is such that every nonzero element has a multiplicative inverse, then it is a field. Although many integral domains, such as the integers Z, do not form a field, every integral domain can be regarded as being contained in a certain field, a field of quotients of the integral domain. For example, the integers are contained in the field Q, the rational numbers, whose elements can all be expressed as quotients of integers.

* A note on notation: Notation is very important in mathematics, witness the notation differences between Newton's and Leibnitz's calculus. Who won out? I've tried to avoid confusion by trying to be as careful as I can with the relevant notation. In particular, [.....] stands for equivalence class or coset, and <.....> for an ideal of a ring. However, in the act of factoring, the ideal takes on the role of zero equivalence class -- the additive identity element -- in the quotient ring thus generated. So, it can be a little confusing. *

Definition:

a is in R

ideal

principle ideal generated by a

"<a>".

An ideal is to a ring as a normal subgroup is to a group.

Definition: Let R be a ring. A polynomial f(x) with coefficients in R is an infinite sum

∑ a_ixⁱ = a₀ + a₁x + ..... + a_nxⁿ + .....,
*[the index i ranges from 0 to ∞]

where a_i is in R and a_i = 0 for all but a finite number of values of i. The a_i are coefficients of f(x).

If F is a field, then F[x] -- the set of all polynomials in an indeterminate x with coefficients in F -- is an integral domain. Note that F[x] is not a field, for x is not a unit in F[x]. An element of a field is a unit of that field if it has a multiplicative inverse; and there is no polynomial f(x) in F[x] such that x•f(x) = 1. For that to be the case, we would have to have the possibility of negative exponents for the x's, which we don't by the definition above.

Definition: Let F be a subfield of a field E, and let α be an element of E. Let f(x) = a₀ + a₁x + ... + a_nxⁿ be in F[x], and let φ_α: F[x} → E be the basic homomorphism taking f(x) to f(α). Let "f(α)" denote

(f(x))φ_α = a₀ + a₁α + ... + a_nαⁿ.

If f(α) = 0, then α is a zero of f(x).

[A homomorphism can be thought of as a map that preserves structure and computational integrity.]

If f(x) has no zero in F, we have to manufacture in some fashion a field E containing F such that there is an α in E with f(α) = (f(x))φ_α = 0. How can we build E? The key is to realize that E is to contain the image (F[x])φ_α of F[x] under our basic homomorphism φ_α.

* It's almost like we're going in the back door to develop F[x] into a field. Find a polynomial that has no zeros or roots in the field F, use it to generate a maximal (principle) ideal, then use this to factor the ring of polynomials thereby constructing a field of polynomials, and by so accomplishing, ensure that all polynomials over the extended field have zeros or solutions. The existence of multiplicative inverses insures the absence of zero divisors, an important feature when factoring. *

Theorem:

R/M

Theorem: (Fundamental Homomorphism Theorem). Let φ be a homomorphism of a ring R into a ring R′ with kernel K. Then Rφ is a ring and there is a canonical isomorphism of Rφ with R/K.

[An isomorphism is a homomorphism that is one-to-one and onto. Intuitively, the domain and its image under an isomorphism contain the same number of elements [cardinality] in their sets and respect the same operations of addition and multiplication. Canonical just means natural in the sense of what one would expect.]

This theorem suggests that we try to form E by forming a factor ring F[x]/N for some suitable ideal N of F[x].

Theorem: F[x]/(p(x)) is a field if and only if p(x) is irreducible.

* Outline of Proof: Given: F[x] is a commutative ring with unity [the multiplicative identity]. We need to show F[x]/(p(x)), for p(x) irreducible, is a field, and in order to do that we need to show that nonzero elements are invertible, that is to say, have inverses. The proof of inverses for non-zero polynomials is too lengthy to include here. It can be found on the page on Quotient Rings below. In the proof, as it turns out, if p(x) is not irreducible, then F[x]/(p(x)) has zero divisors, in which case it fails to even be an integral domain.*

The Complex Number Field: Let F = R, and let f(x) = (x² + 1), which is well known to have no zeros in R, and thus is irreducible over R. Then <x² + 1> is a maximal ideal in R[x], so R[x]/<x² + 1> is a field. Identifying r in R with r + <x² + 1>, we can view R as a subfield of E = R[x]/<x² + 1>. Let

α = x + <x² + 1>. Computing in R[x]/<x² + 1>, we find

α² + 1 = (x + <x² + 1>)² + (1 + <x² + 1>)
= (x² + 1) + <x² + 1> = 0.

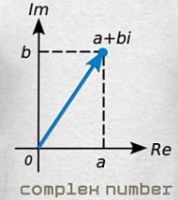
Thus α is a zero of (x² + 1) in R[x]/<x² + 1>. We can view R[x]/<x² + 1> as an extension of R. Then R(α) = R[x]/<x² + 1> and consists of all elements of the form a + bα for a, b in R. But since α² + 1 = 0, we see that α plays the role of i in C, and a + bα plays the role of (a + bi) in C. Therefore R(α) is isomorphic to C.

We're identifying <x² + 1> with zero through the factor ring where the kernel is the zero element, analogous to a factor group, the role of normal subgroup being played by the ideal. The polynomial (x² + 1) has no solution in R, the Real Numbers, but it does in C, the Complex Numbers -- the solution being the square root of minus one, i = √-1.

(x² + 1)φ_α = i² + 1 = 0

We're basically extending the field R to C; that is, in the act of deflating, we expand. The external appearance of R[x] shrinks and at the same instant its internal configuration embeds itself in the newly defined algebraic structure, infusing its integral domain structure into that of the field -- R[x]/<x² + 1>.

This is very similar to how the field of rational numbers, Q, includes the integral domain of integers, Z. Z before the transition is all of the universe, after, it resides inside the more complex Q. Imagine the integers spread out on a line, suddenly the formerly blank space between pairs is filled with an infinite number of fractions -- quotients of integers. By virtue of these fractions, the non-zero integers take on the new role of units. Z shrinks in relative size, yet grows, through sub-divisions, to a vast sea of multi-dimensional relationships and interconnections.

Here's what's happening: The axiom we needed to jump from an integral domain to a field was the existence of a multiplicative inverse for each non-zero polynomial -- f(x) + <p(x)> -- in our quotient ring. Those are our units. A proof that they exist can be found at the link on Quotient Rings below. That gives us the added internal structure of an abelian multiplicative group and hence, a field. The symmetry of connections after collapse increases by a whole new order. Topologically, a refinement has been made.

If you're interested in understanding how Quotient Rings work, what constitutes a coset, etcetera, check out: Quotient Rings | PDF File - Professor Bruce Ikenaga and Quotient Rings of Polynomial Rings.

Here's the beauty and magic of this. Regardless of whether or not you understand the theory, the math, what is going on is quite remarkable. We're creating an extension of an integral domain to a field for purposes of solving an irreducible polynomial, one that's unsolvable in the environment restricted to the real numbers. In the world of algebraic hierarchy, a field is one level above an integral domain in structural identity and therefore in complexity, similar to the difference in atom arrangements between liquid water and ice crystals. So, we're generating a more complex structure by superimposing a conditional symmetry on the parent structure through the process of factoring. A transformation to a new species occurs, one whose interconnections are far more intricate.

By identifying the irreducble polynomial with the zero element of the factor ring, we map all polynomials of the parent ring that contain the irreducble as a factor to the kernel [the maximal ideal], the zero element of the factor ring, our manufactured field. All other non-zero polynomials [units] are considered congruent if they differ by a multiple of the zero-class -- [x² + 1] -- and are thereby grouped into cosets of equivalence classes.

By placing boundaries, setting initial conditions, on something infinite and incomprehensible, we make it comprehensible. To reiterate, by partitioning the ring of polynomials with real number coefficients -- R[x] -- into distinct, disjoint cosets modulo <x² + 1> we are essentially collapsing R[x] by a subring containing all polynomials that share (x² + 1) as a factor -- (x² + 1)•f(x) for all polynomials f(x) in R[x]. Simultaneously we are increasing the complexity of R[x]. We're going from a one-dimensional system -- the Real Numbers -- to a two-dimensional system -- the Complex Numbers.

To paraphrase from above: Then R(i) = R[x]/<x² + 1> and consists of all elements of the form a + bi for a, b in R. The extension creates the vector space of two-dimensions. From this we see that the Complex Number Field is isomorphic to the Euclidean Plane. One axis for the Reals and the other for "i", the imaginary number -- √-1. Any point in the plane-space can thus be mapped by a complex number.

By factoring the parent ring with the stamp of the irreducible polynomial, we force (x² + 1) to equal zero and thereby introduce the number √-1. By increasing the complexity of the integral domain structure, we generate another dimension in the number field. R thus becomes a subfield component of C; that is to say, <R, √-1> is an extension over the fixed field R.

The mathematics of evolution.

For p(x) = (x² + 1):

The real line is the function line, each point, a function or polynomial, f(x). To it is added a function-multiple of i = p(x). The linear combination, f(x) + <p(x)>, maps isomorphically to a + bi on the complex plane.

The field of polynomials, R[x]/<p(x)> equal to R(i) ≈ C can be mapped to the complex plane by cosines and sines.

The exponential function e^iθ equals the sum of the power series expansions for cos(θ) and i sin(θ).

From: e^iθ = cos(θ) + i sin(θ),

We get: e^{i f(x)} = cos(f(x)) + i sin(f(x))

Replacing θ with f(x) in R[x] maps them isomorphically to the complex plane. Each non-zero number on the Real line must equal, or is isomorphic to, a function in R[x].

The zero equivalence class, [p(x)], is orthogonal to the function line, and is therefore at 90 degrees, or π/2 radians. Therefore, for x = 0, the cosine of f(x) + 0[p(x)] equals one, and the sine equals zero. And for a nonzero multiple of [p(x)], the sine [p(x)], or the i axis in the complex plane, is equal to one (1) and the cosine, zero.

e^i[p(x)] = cos([p(x)]) + i sin([p(x)]) = i

Book Review of An Imaginary Tale: The Story of the √-1 | by Paul J.Nahin
Review by Brian E. Blank | PDF File

[Black & White version]